※線形解析では微小ひずみが前提であり、逐次荷重を増分した計算もしないため公称ひずみが用いられる。 非線形解析では逐次荷重を増分させながら解析が実行されるため、ひずみの足し合わせが可能な真ひずみが用いられる。
●公称ひずみ(工学ひずみ)---------------------------------
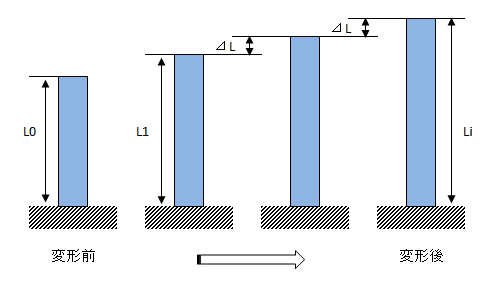
長さの変化分を元の長さL0で割った値。対する応力は公称応力
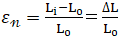
εn:公称ひずみ、L0:変形前長さ、L:変形後長さ
●真ひずみ(対数ひずみ)---------------------------------
長さの変化分を元の長さで割るのは公称ひずみと同じだが、元の長さ基準が異なる。真ひずみでは変形過程を考慮して、元の長さがL0,L1,L2・・・Liと変化していく。対する応力は真応力、コーシー応力とも呼ばれる。
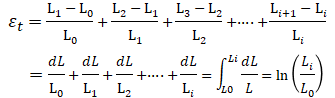
εt:真ひずみ、l0:変形前長さ、l:変形後長さ
◆公称ひずみと真ひずみの違い
【例】L0=100㎜の棒を±120mmまで変化させたときの公称ひずみと真ひずみ
公称ひずみ
引張 :ε=(120-100)/100 =0.20 (=20%)
圧縮 :ε=(80-100)/100 =-0.20 (=-20%)
真ひずみ
引張 : εt=ln(120/100)=ln(1.2)≒0.1823 (=18.2%)
圧縮 : εt=ln(80/100)=ln(0.8)≒-0.223 (-22.3%)
つまり、引張では真ひずみが公称ひずみより小さく、圧縮では真ひずみが公称ひずみより大きくなる(負の方向で)。




