【ミーゼス応力とは】
①ミーゼス応力を簡単に言うと,多軸応力場において,1軸の引張り又は圧縮応力へ投影した値と考えることが出来る. ミーゼス応力は多軸応力場において,降伏点に達したらその材料は降伏すると判断する.
②ミーゼス応力は方向を持たないスカラー値である.そのため圧縮か引張かどうかはミーゼス応力でだけでは判断できない. 最大主応力や最小主応力などは方向を持つベクトル値である.なお、応力はテンソルである.
③延性材料(鋼材)などはミーゼス応力,脆性材料(コンクリートなど)は最大主応力で一般的に評価される.
④ミーゼス応力は相当応力とも言われ,せん断ひずみエネルギーが材料の強度に達した時に降伏する.「せん断ひずみエネルギー説」
⑤ミーゼス応力は最大・中間・最小主応力または6成分の各応力(直応力,せん断応力)から算出されます.
σvm:ミーゼス応力
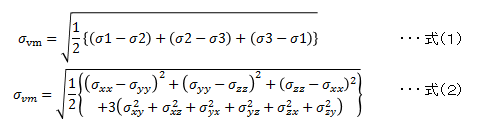
■実際にどういう事かイメージしやすいようにFEM解析を行ってみました.
【検証仮定】〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
・引張100N/mm2で降伏する材料とする.
・全モデルとも上面に鉛直方向の引張荷重を載荷(100N/mm2)
※全モデルともσ1(最大主応力)=100N/mm2
各モデルの条件でエクセル等で式(1)を用い計算すると,
| モデル① | モデル② | モデル③ | |
|---|---|---|---|
| σ1 | 100 | 100 | 100 |
| σ2 | 0 | 50 | 0 |
| σ3 | 0 | 0 | -50 |
| σvm | 100N/mm2 | 86.6N/mm2 | 132.3N/mm2 |
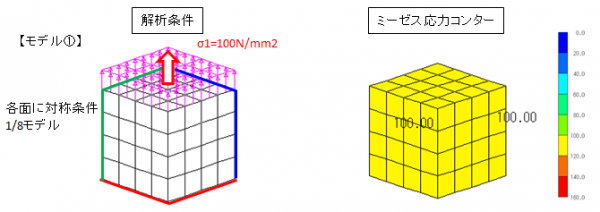
◆モデル①——————————————————
モデル①では,1軸方向に引張が作用しているのみでσ1=ミーゼス応力となる.
※σvm=100N/mm2 で降伏する.
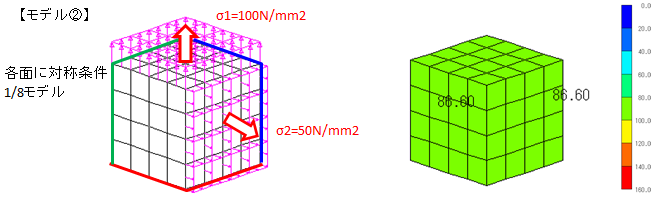
◆モデル②——————————————————–
モデル②で側面に引張応力σ2が作用すると,σ2方向へ延び,σ1方向へは縮む.
全体的に考えるとσ1方向のひずみをσ2が低減させることとなりミーゼス応力はσ1より小さくなる。
※σvm=86.6N/mm2 で降伏しない.
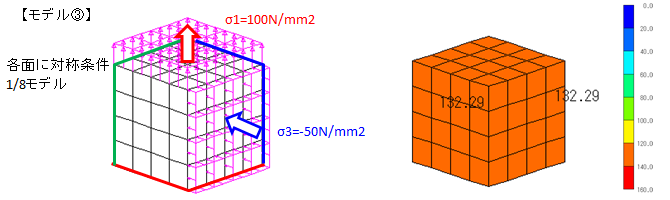
◆モデル③——————————————————–
モデル③で側面に圧縮応力σ3が作用すると,σ3方向へ縮み,σ1方向へは延びる。
全体的に考えるとσ1方向のひずみをσ2が増加させることとなりミーゼス応力はσ1より大きくなる。
※σvm=132.29N/mm2 で降伏する.
以上の事から,1軸方向に引張の降伏荷重程度が作用していても2軸方向に引張が作用していると 降伏しないが、圧縮が作用してる場合は降伏する可能性がある.




